Zadanie nr 2833080

Rozwiąż graﬁcznie układ równań 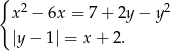{ 2 2 x − 6x = 7+ 2y− y |y− 1| = x + 2.

Rozwiązanie

Przekształćmy pierwsze równanie (zwijamy je o równania okręgu).

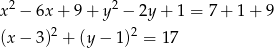
2 2 x − 6x + 9 + y − 2y + 1 = 7+ 1+ 9 (x − 3)2 + (y − 1)2 = 17

Jest to zatem okrąg o środku 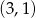(3,1 ) i promieniu √ --- 17 .

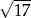Zajmijmy się teraz drugim równaniem. Jeżeli zapiszemy je w postaci

x = |y− 1|− 2

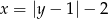
to widać, że jest to wykres funkcji 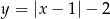y = |x − 1|− 2 , ale narysowany przy zamienionych rolach osi i 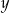. Inny sposób, to rozpisać wartość bezwzględną:

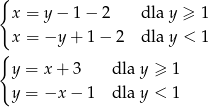
{ x = y − 1 − 2 dla y ≥ 1 {x = −y + 1− 2 dla y < 1 y = x + 3 dla y ≥ 1 y = −x − 1 dla y < 1

Teraz bez trudu rysujemy oba wykresy.

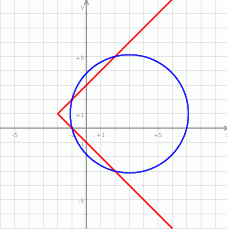
Jeżeli naszkicujemy je dość dokładnie, to można zauważyć, że przecinają się w okolicach punktów

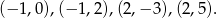
(− 1,0),(− 1,2),(2,− 3),(2,5).

Żeby mieć pewność, że to właśnie te punkty, wstawiamy je do danych równań. Mamy kolejno

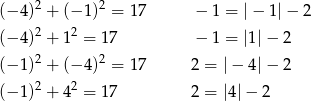
(−4 )2 + (− 1)2 = 17 − 1 = |− 1|− 2 (−4 )2 + 1 2 = 17 − 1 = |1|− 2 2 2 (−1 ) + (− 4) = 17 2 = |− 4|− 2 (−1 )2 + 4 2 = 17 2 = |4|− 2

Podane równości są prawdziwe, co oznacza, że wypisane przez nas punkty są OK.
Odpowiedź: (− 1,0),(− 1,2),(2,− 3),(2,5 )