Zadanie nr 6542258
Rozwiąż algebraicznie i graficznie układ równań 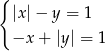 .
.
Rozwiązanie
Zacznijmy od rozwiązania rachunkowego. Mamy cztery możliwe przypadki
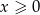 i
i 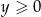
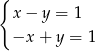
Dodając te równania stronami widać, że układ jest sprzeczny.
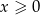 i
i 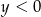
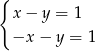
Dodając te równania stronami widać, że
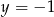 i
i 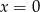 .
. 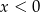 i
i 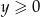
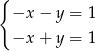
Dodając te równania stronami widać, że
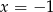 i
i 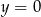 .
. 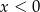 i
i 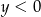
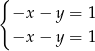
Mamy zatem
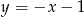 i
i 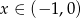 (warunek na
(warunek na  wynika z nierówności
wynika z nierówności 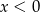 i
i 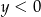 ).
).
Wszystkie podpunkty razem dają rozwiązanie 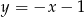 i
i 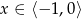 .
.
Teraz pora na rozwiązanie geometryczne. Rysujemy w jednym układzie wpołrzędnych wykresy 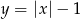 i
i 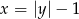 . Pierwszy z tych wykresów to
. Pierwszy z tych wykresów to 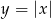 przesunięty o jedna jednostkę w dół, a ten drugi to dokłądnie to samo, ale przy zamienionych osiach
przesunięty o jedna jednostkę w dół, a ten drugi to dokłądnie to samo, ale przy zamienionych osiach  i
i 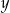 miejscami (wygodnie obrócić sobie kartkę o
miejscami (wygodnie obrócić sobie kartkę o 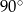 ). Inny sposób narysowania drugiego wykresu to rozbicie go na dwa wzory
). Inny sposób narysowania drugiego wykresu to rozbicie go na dwa wzory 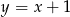 dla
dla 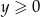 (czyli
(czyli 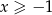 ) oraz
) oraz 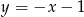 dla
dla 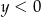 (czyli
(czyli 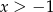 ).
).
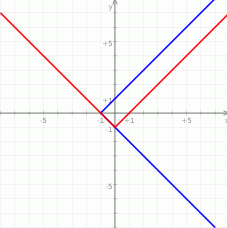
Widać, że wykresy te pokrywają się na przedziale 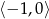
Odpowiedź: 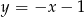 i
i