Zadanie nr 2901142

Wyznacz wszystkie wartości parametru 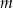, dla których równanie

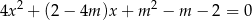
2 2 4x + (2− 4m )x+ m − m − 2 = 0

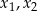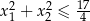ma dwa różne dodatnie rozwiązania x1,x2 spełniające nierówność x12+ x 22 ≤ 147 .

Wersja PDF

Rozwiązanie

Sprawdźmy najpierw kiedy podane równanie ma dwa pierwiastki.

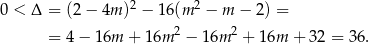
2 2 0 < Δ = (2− 4m) − 16 (m − m − 2) = = 4− 16m + 1 6m 2 − 16m 2 + 16m + 32 = 36.

Skorzystamy teraz ze wzorów Viète’a.

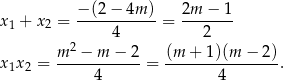
−-(2−--4m-) 2m--−-1 x 1 + x 2 = 4 = 2 2 x 1x2 = m--−--m-−-2-= (m-+--1)(m-−--2). 4 4

Oba pierwiastki będą dodatnie, gdy

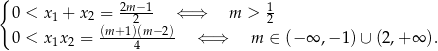
{ 2m− 1 1 0 < x1 + x2 = --2-- ⇐ ⇒ m > 2 0 < x1x2 = (m-+1)(m-−2) ⇐ ⇒ m ∈ (− ∞ ,− 1)∪ (2 ,+ ∞ ). 4

Zatem pierwiastki są dodatnie, gdy

m ∈ (2,+ ∞ ).

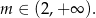
Pozostało rozwiązać nierówność

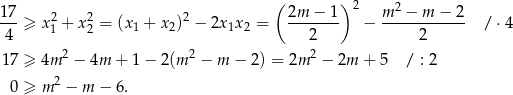
( )2 2 17-≥ x 2+ x 2= (x + x )2 − 2x x = 2m--−-1 − m---−-m-−-2- / ⋅4 4 1 2 1 2 1 2 2 2 2 2 2 17 ≥ 4m − 4m + 1 − 2(m − m − 2) = 2m − 2m + 5 / : 2 0 ≥ m 2 − m − 6.

Rozwiązujemy otrzymaną nierówność kwadratową

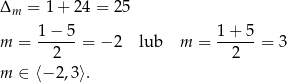
Δm = 1 + 2 4 = 25 1 − 5 1 + 5 m = --2---= − 2 lub m = --2---= 3 m ∈ ⟨− 2,3⟩.

Łącząc ten warunek z warunkiem otrzymanym z dodatniości pierwiastków, mamy

m ∈ (2 ,3⟩.

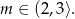
Odpowiedź: m ∈ (2,3⟩