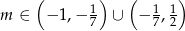/Szkoła średnia/Równania/Kwadratowe/Z parametrem/Znaki pierwiastków

Zadanie nr 4483831

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz te wartości parametru 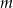m , dla których równanie 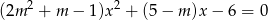(2m 2 + m − 1)x2 + (5− m)x − 6 = 0 ma dwa różne pierwiastki tego samego znaku.

Rozwiązanie

Sprawdźmy najpierw kiedy podane równanie ma dwa różne pierwiastki. Oczywiście musi być kwadratowe, czyli

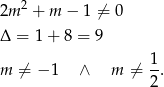
2 2m + m − 1 ⁄= 0 Δ = 1+ 8 = 9 m ⁄= − 1 ∧ m ⁄= 1-. 2

Ponadto

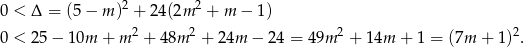
2 2 0 < Δ = (5 − m ) + 24(2m + m − 1) 0 < 2 5− 10m + m 2 + 48m 2 + 24m − 24 = 49m 2 + 14m + 1 = (7m + 1)2.

Zatem 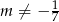m ⁄= − 17 .

Pierwiastki będą miały ten sam znak, jeżeli ich iloczyn jest dodatni. Na mocy wzorów Viète’a mamy więc

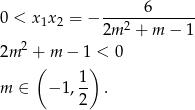
-----6------- 0 < x1x2 = − 2m 2 + m − 1 2 2m +( m − 1)< 0 1 m ∈ − 1,2- .

Skorzystaliśmy oczywiście z wcześniej znalezionego rozkładu trójmianu 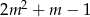2 2m + m − 1 . W połączeniu z warunkiem na 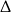Δ -ę, mamy więc

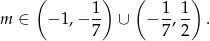
( ) ( ) m ∈ − 1,− 1- ∪ − 1, 1 . 7 7 2

 
Odpowiedź: ( ) ( ) m ∈ − 1,− 1 ∪ − 1, 1 7 7 2

Wersja PDF