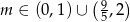/Szkoła średnia/Równania/Kwadratowe/Z parametrem/Znaki pierwiastków

Zadanie nr 8546801

Wyznacz wszystkie wartości parametru 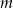m , dla których równanie 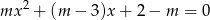mx 2 + (m − 3)x + 2− m = 0 ma dwa rozwiązania dodatnie.

Wersja PDF

Rozwiązanie

Jeżeli 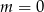m = 0 , to mamy równanie liniowe, które nie może mieć dwóch rozwiązań. Będziemy więc dalej zakładać, że mamy równanie kwadratowe (czyli m ⁄= 0 ).

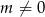Sprawdźmy kiedy równanie ma dwa rozwiązania

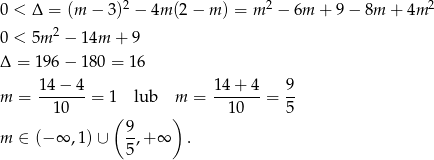
0 < Δ = (m − 3)2 − 4m (2− m ) = m 2 − 6m + 9 − 8m + 4m 2 2 0 < 5m − 14m + 9 Δ = 196 − 18 0 = 16 m = 1-4−--4 = 1 lub m = 1-4+-4-= 9- 1 0 ( ) 10 5 9 m ∈ (− ∞ ,1)∪ 5-,+ ∞ .

Obydwa pierwiastki są dodatnie jeżeli ich suma i iloczyn są dodatnie, czyli na mocy wzorów Viète’a

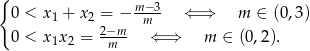
{ 0 < x1 + x2 = − m-−3 ⇐ ⇒ m ∈ (0,3) 2−m- m 0 < x1x2 = m ⇐ ⇒ m ∈ (0 ,2 ).

W połączeniu z warunkiem na 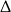Δ -ę, mamy

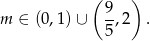
( ) m ∈ (0 ,1 )∪ 9,2 . 5

 
Odpowiedź: m ∈ (0,1)∪ (9,2) 5

Wersja PDF