Zadania.info
Największy internetowy zbiór zadań z matematyki
cornersUpL
cornersUpR

Zadania

Na skróty

Recenzje

Linki sponsorowane

cornersM
Zaloguj się

Linki sponsorowane

cornersR
Zadanie nr 6013219

Dla jakich wartości parametru 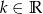k ∈ R zbiory

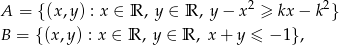
2 2 A = {(x,y) : x ∈ R, y ∈ R , y − x ≥ kx− k } B = { (x,y) : x ∈ R , y ∈ R , x + y ≤ − 1} ,

są rozłączne?

Wersja PDF
Rozwiązanie

Spróbujmy zidentyfikować oba podane zbiory.

Nierówność w definicji zbioru 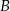B możemy zapisać w postaci 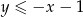y ≤ −x − 1 . Nierówność tę spełniają więc wszystkie punkty leżące poniżej prostej y = −x − 1 .

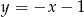Nierówność w definicji zbioru 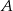A możemy zapisać w postaci

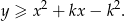
2 2 y ≥ x + kx − k .

Są to więc punkty leżące powyżej paraboli 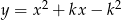2 2 y = x + kx − k .

PIC

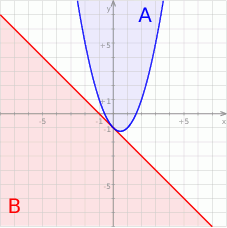
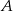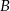W takim razie zbiory A i B będą rozłączne dokładnie wtedy, gdy parabola 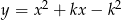y = x2 + kx− k2 leży powyżej prostej 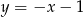y = −x − 1 . Tak będzie, gdy nierówność

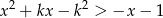
x2 + kx − k2 > −x − 1

będzie spełniona przez każdą liczbę 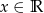x ∈ R . Liczymy

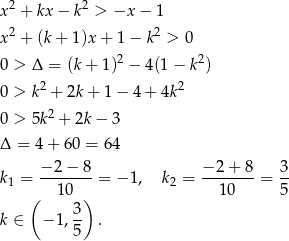
x2 + kx − k2 > −x − 1 2 2 x + (k + 1)x + 1 − k > 0 0 > Δ = (k + 1)2 − 4(1 − k2) 0 > k 2 + 2k + 1 − 4 + 4k2 2 0 > 5k + 2k − 3 Δ = 4 + 60 = 64 − 2− 8 − 2+ 8 3 k1 = -------= − 1, k2 = ------- = -- ( 10 ) 10 5 3- k ∈ − 1,5 .

 
Odpowiedź: ( 3 ) k ∈ − 1,5

Wersja PDF
Twoje uwagi
Nie rozumiesz fragmentu rozwiązania?
W rozwiązaniu jest błąd lub literówka?
Masz inny pomysł na rozwiązanie tego zadania?
Napisz nam o tym!