Zadanie nr 8004268
Zaznacz w układzie współrzędnych zbiór punktów, których współrzędne 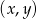 są rozwiązaniem układu nierówności
są rozwiązaniem układu nierówności
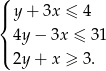
Oblicz pole tego obszaru.
Rozwiązanie
Plan jest prosty: szkicujemy proste 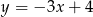 ,
, 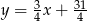 oraz
oraz 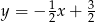 , a potem zaznaczamy obszar, który jest jednocześnie poniżej dwóch pierwszych prostych i powyżej trzeciej prostej. Zanim to jednak zrobimy wyznaczmy współrzędne punktów wspólnych tych trzech prostych. Powiedzmy, że pierwsze dwie przecinają się w punkcie
, a potem zaznaczamy obszar, który jest jednocześnie poniżej dwóch pierwszych prostych i powyżej trzeciej prostej. Zanim to jednak zrobimy wyznaczmy współrzędne punktów wspólnych tych trzech prostych. Powiedzmy, że pierwsze dwie przecinają się w punkcie 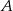 , druga z trzecią w punkcie
, druga z trzecią w punkcie 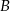 , a trzecia z pierwszą w punkcie
, a trzecia z pierwszą w punkcie 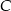 .
.
Wyznaczamy współrzędne punktu 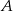 .
.
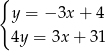
Dodajemy równania stronami (żeby zredukować  ) i mamy
) i mamy 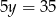 , czyli
, czyli 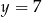 i
i 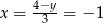 . Zatem
. Zatem 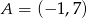 .
.
Wyznaczamy współrzędne punktu 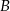 .
.
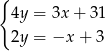
Odejmujemy od pierwszego równania drugie pomnożone przez 2 (żeby zredukować 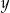 ) i mamy
) i mamy 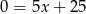 , czyli
, czyli 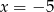 i
i 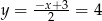 . Zatem
. Zatem 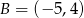 .
.
Wyznaczamy współrzędne punktu 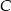 .
.
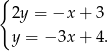
Odejmujemy od pierwszego równania drugie pomnożone przez 2 (żeby zredukować 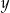 ) i mamy
) i mamy 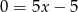 , czyli
, czyli 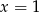 i
i 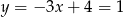 . Zatem
. Zatem 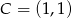 .
.
Teraz jesteśmy w stanie wykonać już dość dokładny rysunek.
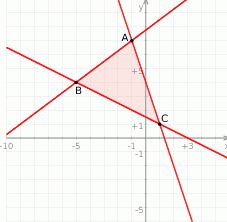
Pole otrzymanego trójkąta obliczymy na dwa sposoby.
Sposób I
Policzymy długość odcinka 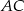 oraz długość wysokości opuszczonej z wierzchołka
oraz długość wysokości opuszczonej z wierzchołka 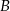 , czyli odległość punktu
, czyli odległość punktu 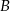 od prostej
od prostej 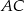 .
.

Teraz liczymy odległość punktu 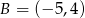 od prostej
od prostej 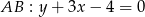 .
.
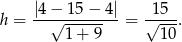
Zatem pole jest równe
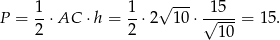
Sposób II
Tym razem skorzystamy ze wzoru na pole trójkąta o wierzchołkach 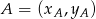 ,
, 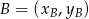 i
i 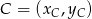 .
.
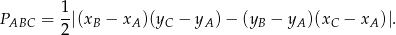
W naszej sytuacji mamy
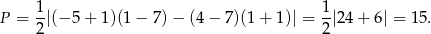
Odpowiedź: 15

