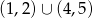/Szkoła średnia/Nierówności/Logarytmiczne/Rozwiąż nierówność

Zadanie nr 8220868

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż nierówność:

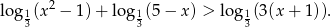
2 log 13(x − 1)+ lo g13(5 − x) > log 13(3(x + 1)).

Rozwiązanie

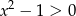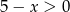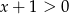Zacznijmy od wyznaczenia dziedziny podanego wyrażenia. Argumenty logarytmów muszą być dodanie, czyli x 2 − 1 > 0 , 5 − x > 0 oraz x + 1 > 0 . Jak zaznaczymy te zbiory na osi liczbowej (rysunek), to widać, że dziedziną nierówności jest przedział (1,5 ) .

PIC

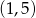Przekształcamy nierówność korzystając ze wzoru 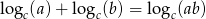lo gc(a)+ lo gc(b) = logc(ab) :

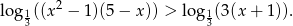
log1((x 2 − 1)(5 − x )) > lo g1(3(x + 1)). 3 3

Możemy teraz opuścić logarytmy, ale ponieważ podstawa jest mniejsza od 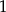1 , to zmieniamy znak nierówności na przeciwny.

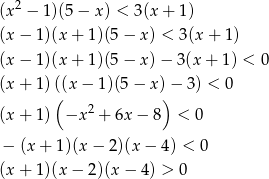
(x 2 − 1 )(5− x) < 3(x + 1) (x − 1)(x+ 1)(5− x) < 3(x + 1 ) (x − 1)(x+ 1)(5− x)− 3(x + 1) < 0 (x + 1)((x − 1)(5 − x) − 3) < 0 ( 2 ) (x + 1) −x + 6x − 8 < 0 − (x + 1)(x − 2)(x− 4) < 0 (x + 1)(x− 2)(x − 4) > 0

Ostatnią nierówność rozwiązujemy znanymi sobie metodami (różni nauczyciele uczą różnych sposobów). My rozwiążemy to metodą węża - rysunek.

PIC

Tak czy inaczej rozwiązaniem tej nierówności jest zbiór 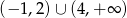(− 1,2)∪ (4 ,+ ∞ ) . Na zakończenie musimy uwzględnić dziedzinę nierówności co daje nam zbiór (1,2) ∪ (4,5) .  
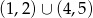Odpowiedź: (1,2) ∪ (4,5)

Wersja PDF