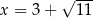Zadanie nr 1099501
Rozwiąż równanie 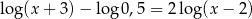 .
.
Rozwiązanie
Aby równanie miało sens musimy mieć
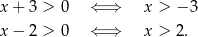
Zatem 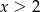 . Korzystamy teraz ze wzoru na różnicę logarytmów.
. Korzystamy teraz ze wzoru na różnicę logarytmów.
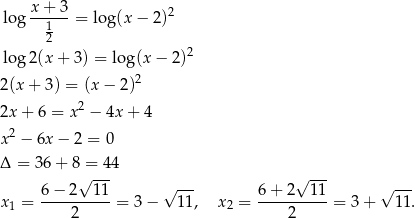
Ujemny pierwiastek odrzucamy i mamy 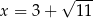 .
.
Odpowiedź: 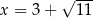
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Rozwiąż równanie 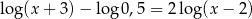 .
.
Aby równanie miało sens musimy mieć
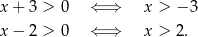
Zatem 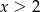 . Korzystamy teraz ze wzoru na różnicę logarytmów.
. Korzystamy teraz ze wzoru na różnicę logarytmów.
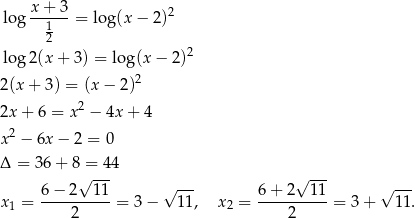
Ujemny pierwiastek odrzucamy i mamy 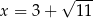 .
.
Odpowiedź: