/Szkoła średnia/Równania/Logarytmiczne

Zadanie nr 1625340

W prostokątnym układzie współrzędnych zaznacz zbiór wszystkich punktów płaszczyzny, których współrzędne spełniają warunek 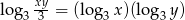xy lo g3 3-= (lo g3x )(log 3y) .

Wersja PDF

Rozwiązanie

Aby logarytmy miały sens musi być 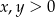x ,y > 0 . Liczymy

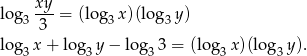
xy log3 -3-= (lo g3x )(log 3y) log3 x+ lo g3y − log3 3 = (log3 x)(log3y ).

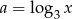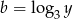Żeby się nie pogubić, podstawmy a = lo g3x i b = lo g3y .

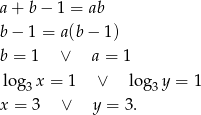
a + b − 1 = ab b − 1 = a(b − 1 ) b = 1 ∨ a = 1 log 3x = 1 ∨ lo g3y = 1 x = 3 ∨ y = 3.

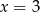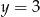Szukany zbiór to zatem kawałki prostych x = 3 i y = 3 zawarte w pierwszej ćwiartce.

PIC

Wersja PDF