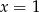/Szkoła średnia/Równania/Logarytmiczne

Zadanie nr 1860470

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż równanie 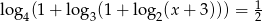1 log4(1 + log3(1 + log2(x + 3 ))) = 2 .

Rozwiązanie

Powinniśmy zacząć od ustalenia jaka jest dziedzina równania. Zamiast to robić, na końcu sprawdzimy poprawność otrzymanych rozwiązań.

Liczymy

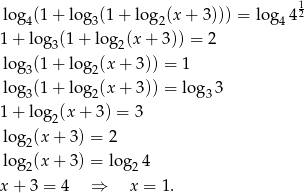
1 log 4(1+ log 3(1+ log 2(x+ 3))) = log4 42 1 + log3(1 + log2(x + 3)) = 2 log 3(1+ log 2(x+ 3)) = 1 log 3(1+ log 2(x+ 3)) = log33 1 + log2(x + 3) = 3 log (x+ 3) = 2 2 log 2(x+ 3) = log24 x + 3 = 4 ⇒ x = 1.

Łatwo sprawdzić poprawność tego rozwiązania.  
Odpowiedź: x = 1

Wersja PDF