Rozwiązywanie równań i nierówności wykładniczych/logarytmicznych bardzo przypomina analogiczną zabawę z funkcjami trygonometrycznymi – też mamy kilka wzorków, dzięki którym musimy sprowadzić takie równanie/nierówność do prostej postaci. Cała sytuacja jest jednak o wiele prostsza, bo nie ma okresowości i wzorów redukcyjnych. Proste równania i nierówności wykładnicze Proste równania wykładnicze to równania postaci
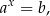
gdzie 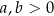 i
i 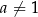 . Nie ma tu żadnego problemu: logarytmujemy stronami logarytmem przy podstawie
. Nie ma tu żadnego problemu: logarytmujemy stronami logarytmem przy podstawie  i mamy
i mamy 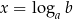 .
.
Rozwiążmy równanie 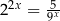 .
.
Liczymy
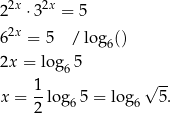
Często jest tak, że równanie ma jeszcze prostszą postać:
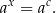
Wtedy możemy od razu wywnioskować, że 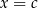 (dzięki różnowartościowości
(dzięki różnowartościowości
funkcji wykładniczej).
Rozwiążmy równanie 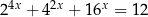 . Liczymy
. Liczymy
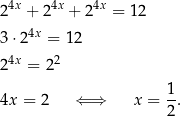
Analogicznie postępujemy w przypadku nierówności tego typu. Jedyna rzecz, na którą musimy uważać, to zmiana znaku nierówności w przypadku, gdy 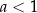 .
.
Rozwiążmy nierówność 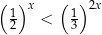 .
.
Liczymy
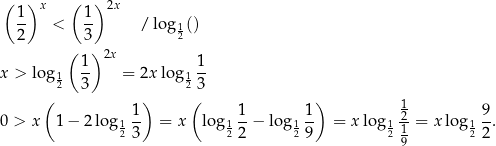
Ponieważ 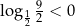 otrzymujemy stąd
otrzymujemy stąd 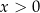 .
.
Sprawdźmy dla jakiej wartości parametru 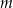 rozwiązaniem nierówności
rozwiązaniem nierówności
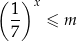
jest przedział 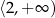 .
.
Liczymy
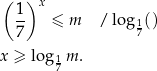
Musimy zatem mieć
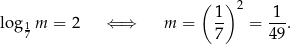
Proste równania i nierówności logarytmiczne Proste równanie logarytmiczne to równanie postaci
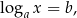
gdzie 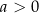 i
i 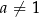 . Rozwiązanie równania tego typu sprowadza się do przypomnienia sobie definicji logarytmu. Powyższa równość oznacza, że
. Rozwiązanie równania tego typu sprowadza się do przypomnienia sobie definicji logarytmu. Powyższa równość oznacza, że
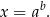
Rozwiążmy równanie 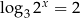 . Liczymy
. Liczymy
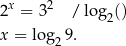
Podobnie jak w przypadku prostych równań wykładniczych, czasem równanie jest jeszcze prostsze:
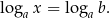
w takiej sytuacji od razu wnioskujemy, że 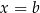 (korzystamy z różnowartościowości
(korzystamy z różnowartościowości
funkcji wykładniczej).
Rozwiążmy równanie 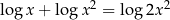 .
.
Liczymy
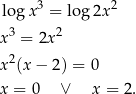
Ze względu na dziedzinę równania jedynym rozwiązaniem jest 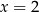 .
.
Przejście od równań do nierówności jest prawie natychmiastowe. Prawie, bo jak zwykle musimy uważać na monotoniczność funkcji logarytmicznej.
Rozwiążmy nierówność 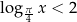 .
.
Zamieniamy 2 z prawej strony na logarytm.
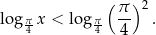
Teraz chcemy opuścić logarytmy. Ponieważ 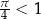 , zmieniamy znak nierówności na przeciwny.
, zmieniamy znak nierówności na przeciwny.
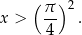
Podstawianie W przypadku bardziej skomplikowanych równań i nierówności wykładniczych lub logarytmicznych niezwykle użyteczną metodą jest podstawienie 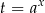 lub
lub 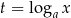 . Bardzo często otrzymujemy w ten sposób równanie/nierówność, które już nie jest wykładnicze/logarytmiczne (zwykle jest wielomianowe).
. Bardzo często otrzymujemy w ten sposób równanie/nierówność, które już nie jest wykładnicze/logarytmiczne (zwykle jest wielomianowe).
Rozwiążmy nierówność 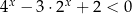 .
.
Podstawiamy 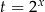 i mamy
i mamy
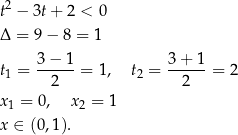
Rozwiążmy równanie 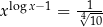 .
.
Logarytmujemy obie strony logarytmem dziesiętnym.
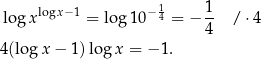
Podstawiamy teraz 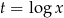 .
.
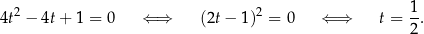
Mamy stąd 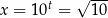 .
.

