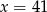Zadanie nr 7871261
Rozwiąż równanie 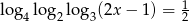 .
.
Rozwiązanie
Liczymy
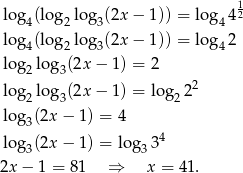
Na koniec sprawdzamy, że 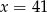 rzeczywiście spełnia dane równanie (musimy to zrobić, bo nie wyznaczyliśmy dziedziny równania).
rzeczywiście spełnia dane równanie (musimy to zrobić, bo nie wyznaczyliśmy dziedziny równania).
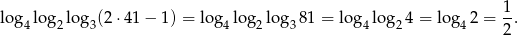
Odpowiedź: 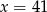
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Rozwiąż równanie 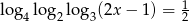 .
.
Liczymy
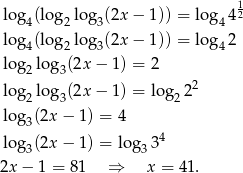
Na koniec sprawdzamy, że 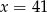 rzeczywiście spełnia dane równanie (musimy to zrobić, bo nie wyznaczyliśmy dziedziny równania).
rzeczywiście spełnia dane równanie (musimy to zrobić, bo nie wyznaczyliśmy dziedziny równania).
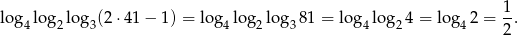
Odpowiedź: