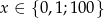Zadanie nr 8710997
Rozwiąż równanie 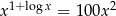 .
.
Rozwiązanie
Ponieważ  jest pod logarytmem, musimy mieć
jest pod logarytmem, musimy mieć 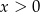 (jest to dziedzina równania). Logarytmujemy obie strony logarytmem przy podstawie 10.
(jest to dziedzina równania). Logarytmujemy obie strony logarytmem przy podstawie 10.
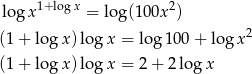
Podstawmy 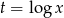 .
.
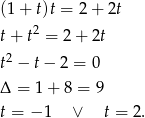
Mamy zatem
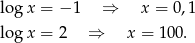
Odpowiedź: 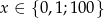
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Rozwiąż równanie 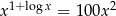 .
.
Ponieważ  jest pod logarytmem, musimy mieć
jest pod logarytmem, musimy mieć 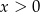 (jest to dziedzina równania). Logarytmujemy obie strony logarytmem przy podstawie 10.
(jest to dziedzina równania). Logarytmujemy obie strony logarytmem przy podstawie 10.
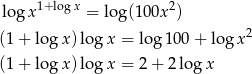
Podstawmy 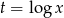 .
.
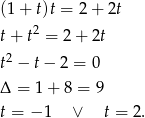
Mamy zatem
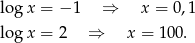
Odpowiedź: