Zadanie nr 9744247
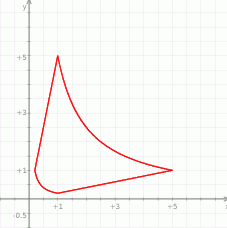
W prostokątnym układzie współrzędnych zaznacz zbiór wszystkich punktów, których współrzędne spełniają warunek 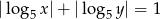 .
.
Rozwiązanie
Oczywiście musi być 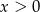 i
i 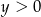 .
.
Żeby opuścić wartości bezwzględne musimy wiedzieć jakie są znaki logarytmów. Z tego powodu rozważmy cztery przypadki.
Jeżeli 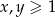 to logarytmy są nieujemne i mamy warunek
to logarytmy są nieujemne i mamy warunek
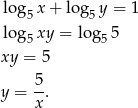
Szkicujemy zatem pierwszy fragment interesującego nas zbioru – jest to fragment hiperboli 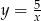 od punktu
od punktu 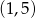 do
do 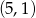
Jeżeli 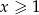 , ale
, ale 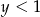 to mamy
to mamy
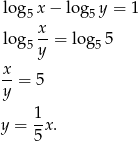
Rysujemy zatem fragment prostej 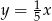 od punktu
od punktu 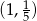 do punktu
do punktu 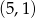 .
.
Jeżeli 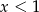 , ale
, ale 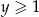 to mamy
to mamy
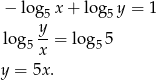
Rysujemy kawałek prostej 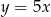 od punktu
od punktu 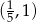 do punktu
do punktu 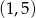 .
.
Jeżeli wreszcie 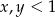 to mamy
to mamy
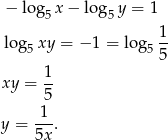
Rysujemy teraz fragment hiperboli 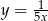 od punktu
od punktu 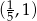 do
do 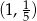 .
.