Zadania.info
Największy internetowy zbiór zadań z matematyki
cornersUpL
cornersUpR

Zadania

Na skróty

Recenzje

Linki sponsorowane

cornersM
Zaloguj się

Linki sponsorowane

cornersR
Zadanie nr 2030352

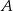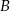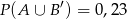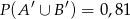Prawdopodobieństwa zdarzeń A i B oraz zdarzeń do nich przeciwnych spełniają warunki: P (A ∪ B ′) = 0,23 i P(A ′ ∪ B ′) = 0,81 .

  • Oblicz P(B ) .
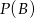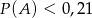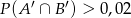  • Wykaż, że jeżeli P(A ) < 0,21 to P(A ′ ∩ B ′) > 0,02 .
Wersja PDF
Rozwiązanie
  • Rysujemy diagram Venna.
    PIC

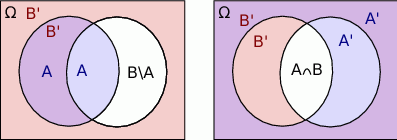
    Z obrazka można odczytać, że

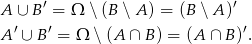
    A ∪ B′ = Ω ∖ (B ∖ A ) = (B ∖A )′ ′ ′ ′ A ∪ B = Ω ∖ (A ∩ B ) = (A ∩ B ).

    Mamy zatem

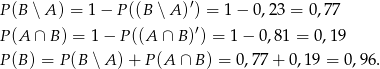
    P(B ∖ A) = 1− P((B ∖ A)′) = 1 − 0,23 = 0,77 P(A ∩ B ) = 1 − P((A ∩ B)′) = 1 − 0,81 = 0,19 P(B ) = P(B ∖ A )+ P (A ∩ B ) = 0,77 + 0,19 = 0,96.

     
    Odpowiedź: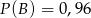 P(B ) = 0,96

  • Patrząc ponownie na diagram Venna można zauważyć, że 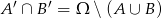′ ′ A ∩ B = Ω ∖(A ∪ B) . Zatem
    ′ ′ P(A ∩ B ) = 1− P(A ∪ B ) = 1 − (P (A) + P (B) − P(A ∩ B)) = = 1 − P (A) − 0,96 + 0,1 9 = 0,23 − P (A) > 0,23− 0,21 = 0,02 .
Wersja PDF
Twoje uwagi
Nie rozumiesz fragmentu rozwiązania?
W rozwiązaniu jest błąd lub literówka?
Masz inny pomysł na rozwiązanie tego zadania?
Napisz nam o tym!