Zadanie nr 2817480
Uzasadnij, że
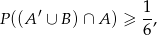
jeżeli 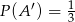 i
i 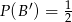 .
.
Rozwiązanie
Sposób I
Rysujemy sobie obrazek i patrzymy czym jest interesujący nas zbiór.
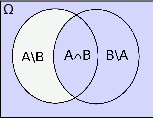
Na obrazku zaznaczyliśmy zbiór 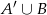 . Powinno być jasne, że jak weźmiemy jego część wspólną z
. Powinno być jasne, że jak weźmiemy jego część wspólną z 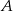 to otrzymamy
to otrzymamy 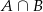 . Zatem
. Zatem
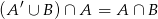
i mamy pokazać nierówność
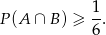
Przekształcamy nierówność dalej korzystając ze wzoru
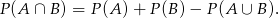
Mamy więc
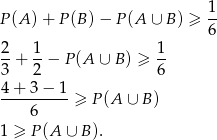
Otrzymana nierówność jest oczywiście prawdziwa, a przekształcaliśmy nierówność w sposób równoważnościowy (tzn. możemy przekształcenia zapisać w odwrotnej kolejności), więc wyjściowa nierówność też jest prawdziwa.
Sposób II
Korzystamy ze wzoru
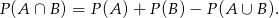
Liczymy
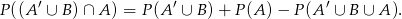
Ostatnie prawdopodobieństwo to oczywiście 1 (bo w nawiasie mamy sumę 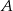 i
i 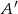 ), więc
), więc
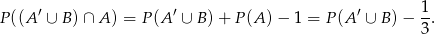
Musimy zatem wykazać nierówność
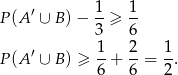
To jest jednak oczywiste, bo 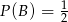 i
i 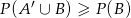 .
.
Sposób III
Korzystamy ze wzoru
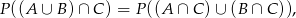
który łatwo sobie uzasadnić na diagramie Venna. W naszej sytuacji mamy
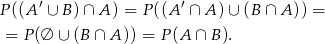
Dalej liczymy jak w I sposobie.

