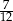Zadanie nr 5781253
W pudełku znajduje się 6 kul czarnych i 4 kule białe. Rzucamy dwa razy monetą. Jeśli otrzymamy 2 orły, losujemy z pudełka kolejno bez zwracania 2 kule. W pozostałych przypadkach losujemy jedną kulę. Oblicz prawdopodobieństwo, że wśród wylosowanych kul jest dokładnie jedna kula czarna.
Rozwiązanie
Prawdopodobieństwo otrzymania 2 orłów, przy dwóch rzutach monetą to 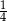 . W tej sytuacji losujemy dwie kule spośród 10, co możemy zrobić na
. W tej sytuacji losujemy dwie kule spośród 10, co możemy zrobić na
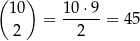
sposobów. Prawdopodobieństwo otrzymania wśród tych kul jednej czarnej jest równe
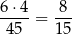
(na 6 sposobów wybieramy kulę czarną i na 4 sposoby kulę białą).
Jeżeli natomiast nie wyrzucimy dwóch orłów, to losujemy jedną kulę spośród 10 i prawdopodobieństwo otrzymania kuli czarnej jest równe
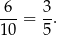
Na mocy wzoru na prawdopodobieństwo całkowite, interesujące nas prawdopodobieństwo jest więc równe
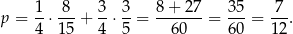
Jeżeli ktoś woli, to rozwiązanie można łatwo zilustrować drzewkiem.
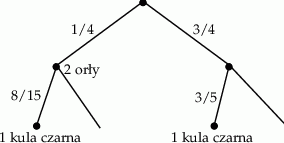
Odpowiedź: