Zadanie nr 6064059
- Wpuszczony do labiryntu szczur, dochodząc do rozwidlenia dróg, dwa razy częściej skręca w lewo niż w prawo. Jakie jest prawdopodobieństwo tego, że dotrze do pokarmu (oznaczonego na rysunku
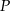 )?
)? 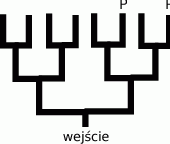
- Inny szczur wpuszczony do tego samego labiryntu, dochodząc do rozwidlenia dróg, skręca w prawo w
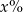 przypadków. Oblicz
przypadków. Oblicz  , jeśli prawdopodobieństwo tego, że dotrze do pokarmu, jest równe
, jeśli prawdopodobieństwo tego, że dotrze do pokarmu, jest równe 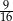 .
.
Rozwiązanie
- Za każdym rozwidleniem podpiszemy prawdopodobieństwa z jakimi szczur wybiera odpowiednie drogi (czyli
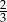 dla lewej i
dla lewej i 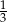 dla prawej).
dla prawej). 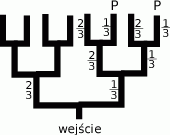
Otrzymujemy w ten sposób drzewko i aby odczytać jakie jest prawdopodobieństwo dojścia do
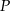 musimy pomnożyć liczby występujące na prowadzących do
musimy pomnożyć liczby występujące na prowadzących do 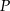 krawędziach. Mamy zatem
krawędziach. Mamy zatem 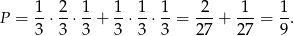
Odpowiedź: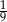
- Licząc podobnie jak poprzednio (teraz prawdopodobieństwa wynoszą
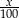 dla prawej strony i
dla prawej strony i 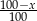 dla lewej), mamy
dla lewej), mamy 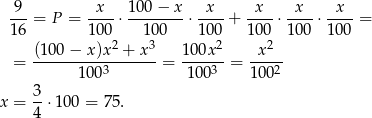
Odpowiedź: