/Szkoła średnia/Prawdopodobieństwo/Warunkowe i całkowite/Różne

Zadanie nr 7838656

Dodaj do ulubionych
Dodaj do rozwiązanych

Dwa zakłady pracy produkują takie same akumulatory, przy czym stosunek liczby akumulatorów produkowanych dziennie przez pierwszy zakład do liczby akumulatorów produkowanych dziennie przez drugi zakład jest równy 2 3 . Badania wykazały, że niektóre z wyprodukowanych akumulatorów mają podwyższoną pojemność, przy czym własność tą ma 40% akumulatorów pochodzących z pierwszego zakładu i 30% akumulatorów pochodzących z drugiego zakładu. Oblicz jakie jest prawdopodobieństwo, że losowo wybrany akumulator pochodzący z dziennej produkcji obu zakładów nie ma podwyższonej pojemności.

Rozwiązanie

Jeżeli oznaczymy przez 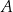A prawdopodobieństwo wybrania akumulatora o podwyższonej pojemności, a przez 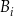Bi prawdopodobieństwo wybrania akumulatora z zakładu o numerze 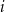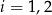i , i = 1 ,2 , to

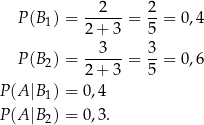
--2--- 2- P (B1) = 2+ 3 = 5 = 0,4 3 3 P (B2) = ------= --= 0,6 2+ 3 5 P(A |B1) = 0 ,4 P(A |B ) = 0 ,3 . 2

Sposób I

Interesuje nas prawdopodobieństwo (korzystamy ze wzoru na prawdopodobieństwo całkowite)

P(A ′) = 1− P(A ) = 1 − [P(A |B )P (B )+ P(A |B )P (B )] = 1 1 2 2 = 1− 0,4⋅0 ,4− 0,3⋅0 ,6 = 0,66.

Sposób II

Zauważmy, że

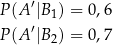
′ P (A |B1) = 0 ,6 P (A ′|B2) = 0 ,7

Zatem interesujące nas prawdopodobieństwo jest równe

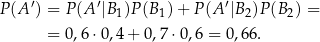
P(A ′) = P(A ′|B1)P(B 1)+ P(A ′|B 2)P(B 2) = = 0,6 ⋅0,4+ 0,7 ⋅0,6 = 0,66.

 
Odpowiedź: 0,66

Wersja PDF