/Szkoła średnia/Prawdopodobieństwo/Warunkowe i całkowite/Karty

Zadanie nr 2489499

Dodaj do ulubionych
Dodaj do rozwiązanych

Z talii 24 kart wyjęto losowo 1 kartę i odłożono na bok. Następnie wylosowano 2 karty. Oblicz prawdopodobieństwo, że za drugim razem wylosowano 2 kiery.

Rozwiązanie

W tali jest 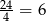24 4 = 6 kierów. Najprościej narysować sobie drzewko, którego pierwszy wiersz odpowiada zdarzeniom 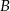B : za pierwszym razem wyciągnięto kiera i 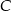C : za pierwszym razem wyciągnięto kartę inną niż kier.

PIC

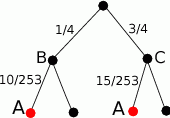
W drugim rzędzie na czerwono zaznaczyliśmy interesujące nas zdarzenie A: za drugim razem wyciągnięto dwa kiery. Prawdopodobieństwa zdarzenia 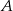A są odpowiednio równe

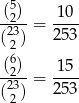
(5) 1 0 -223--= ---- (2) 253 (6) 1 5 -2--= ---- (232) 253

Mamy zatem

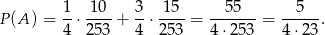
1- 10-- 3- 15-- --55--- --5--- P(A ) = 4 ⋅ 253 + 4 ⋅ 253 = 4⋅25 3 = 4 ⋅23 .

Uważny czytelnik może zauważyć, że ostatni wzór to wzór na prawdopodobieństwo całkowite. Tak też mogliśmy zrobić to zadanie: trzeba rozważać zdarzenia ’za drugim razem wylosowano dwa kiery pod warunkiem, że za pierwszym razem był kier’ i ’...pod warunkiem, że za pierwszym razem nie był kier’. Potem wystarczy zastosować wzór na prawdopodobieństwo całkowite.  
Odpowiedź: -5 92

Wersja PDF