Zadanie nr 6245989
Z talii 52 kart w czterech kolorach wybieramy losowo 2 karty. Oblicz prawdopodobieństwo, że wybrane karty to król i as, przy założeniu, że wybrane karty mają różne kolory.
Rozwiązanie
Dwie karty możemy wybrać z talii na
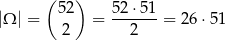
sposobów.
Oznaczmy przez 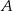 zdarzenie polegające na wybraniu króla i asa, a przez
zdarzenie polegające na wybraniu króla i asa, a przez 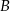 zdarzenie polegające na wybraniu kart w różnych kolorach. Musimy więc obliczyć
zdarzenie polegające na wybraniu kart w różnych kolorach. Musimy więc obliczyć
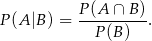
Ponieważ w talii są 4 króle i 4 asy, jest
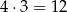
zdarzeń sprzyjających zdarzeniu 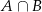 (na 4 sposoby możemy wybrać króla i na 3 sposoby możemy wybrać asa w innym kolorze niż król).
(na 4 sposoby możemy wybrać króla i na 3 sposoby możemy wybrać asa w innym kolorze niż król).
Prawdopodobieństwo zdarzenia 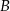 obliczymy na kilka sposobów.
obliczymy na kilka sposobów.
Sposób I
Jeżeli chcemy wybrać dwie karty w różnych kolorach, to najpierw wybieramy te dwa kolory – możemy to zrobić na
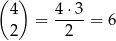
sposobów. Potem wybieramy po jednej karcie w każdym z tych kolorów, co w sumie daje nam
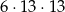
różnych możliwości.
Interesujące nas prawdopodobieństwo jest więc równe
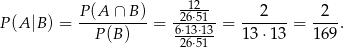
Sposób II
Jeżeli chcemy wybrać dwie karty w różnych kolorach, to pierwszą kartę wybieramy dowolnie, a drugą wybieramy tak, aby nie była w tym samym kolorze – możemy to zrobić na
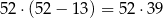
sposobów. Ten rachunek jest jednak błędny, bo każdą parę kart policzyliśmy dwa razy – aby go poprawić musimy wynik podzielić przez 2. Jest więc
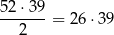
możliwości wybrania dwóch kart w różnych kolorach.
Interesujące nas prawdopodobieństwo 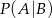 obliczamy tak samo jak w poprzednim sposobie.
obliczamy tak samo jak w poprzednim sposobie.
Sposób III
Tym razem zamiast obliczyć liczbę zdarzeń sprzyjających zdarzeniu 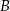 obliczymy liczbę zdarzeń sprzyjających zdarzeniu przeciwnemu
obliczymy liczbę zdarzeń sprzyjających zdarzeniu przeciwnemu 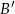 , tzn. zdarzeniu, w którym wybraliśmy dwie karty w tym samym kolorze. Dwie karty w tym samym kolorze możemy wybrać na
, tzn. zdarzeniu, w którym wybraliśmy dwie karty w tym samym kolorze. Dwie karty w tym samym kolorze możemy wybrać na
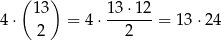
sposobów (na 4 sposoby wybieramy kolor i potem wybieramy 2 karty w tym kolorze). Zdarzeń sprzyjających zdarzeniu 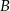 jest więc
jest więc
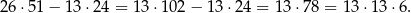
Interesujące nas prawdopodobieństwo 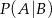 obliczamy tak samo jak w pierwszym sposobie.
obliczamy tak samo jak w pierwszym sposobie.
Odpowiedź: