/Szkoła średnia/Prawdopodobieństwo/Warunkowe i całkowite/Kostki

Zadanie nr 2394024

Dodaj do ulubionych
Dodaj do rozwiązanych

W pudełku znajdują się 4 kostki do gry: 3 sześcienne (ze ścianami ponumerowanymi liczbami od 1 do 6) i jedna czworościenna (ze ścianami ponumerowanymi liczbami od 1 do 4). Losowo wybrano kostkę, wykonano nią 3 rzuty i w wyniku tych 3 rzutów otrzymano trzy razy jedynkę. Jakie jest prawdopodobieństwo, że wybrana kostka była kostką czworościenną?

Rozwiązanie

Prawdopodobieństwo otrzymania 3 jedynek przy użyciu kostki sześciennej jest równe

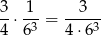
3-⋅-1-= --3-- 4 63 4 ⋅63

(kostkę sześcienną możemy wybrać z prawdopodobieństwem 3 4 , a potem jest tylko jedno zdarzenie sprzyjające). Analogicznie, prawdopodobieństwo otrzymania 3 jedynek przy użyciu kostki czworościennej jest równe

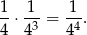
1-⋅-1-= -1. 4 4 3 44

Wśród wszystkich zdarzeń, w których wypadły 3 jedynki zdarzenia odpowiadające czworościennej kostce stanowią

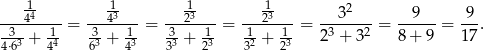
414 143- 213 123 32 9 9 -3-----1-= -3---1- = 3----1-= -1----1 = -3----2 = ------= ---. 4⋅63 + 44 63 + 43 33 + 23 32 + 23 2 + 3 8 + 9 17

Jeżeli chcemy zapisać powyższy warunek przy pomocy prawdopodobieństwa warunkowego, to oznaczmy przez 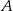A zdarzenie polegające na wybraniu kostki czworościennej, a przez 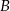B zdarzenie polegające na wylosowaniu 3 jedynek. Przy tych oznaczeniach interesujące nas prawdopodobieństwo to prawdopodobieństwo warunkowe

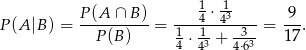
1 -1 P (A|B ) = P(A--∩-B)-= ---4-⋅43----= 9-. P (B) 14 ⋅ 13 +-33- 17 4 4⋅6

 
Odpowiedź: -9 17

Wersja PDF