Zadanie nr 6173916
Rzucamy dwukrotnie kostką do gry. Jakie jest prawdopodobieństwo, że suma wyrzuconych oczek jest większa niż 9, jeżeli wiadomo, że dokładnie jeden raz wypadło 6 oczek?
Rozwiązanie
Sposób I
Jeżeli wiemy, że dokładnie na jednej z kostek wypadło 6 oczek, to za zdarzenia elementarne możemy przyjąć pary postaci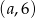 
i 
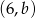, gdzie 
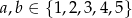. Jest więc
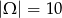
zdarzeń elementarnych. Są 4 zdarzenia sprzyjające:
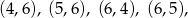
więc interesujące nas prawdopodobieństwo jest równe
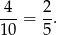
Sposób II
Tym razem skorzystamy ze wzoru
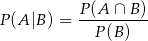
na prawdopodobieństwo warunkowe.
Za zdarzenia elementarne przyjmijmy pary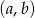 
otrzymanych oczek, czyli
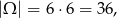
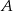niech będzie zdarzeniem polegającym na otrzymaniu sumy oczek większej niż 9, a 
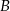nie będzie zdarzeniem polegającym na otrzymaniu dokładnie na jednej kostce szóstki. Mamy zatem
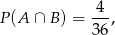
bo są 4 zdarzenia, w których na jednej z kostek jest 6 i jednocześnie suma oczek na dwóch kostkach jest większa niż 9:
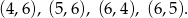
Ponadto jest 10 zdarzeń sprzyjających 
– są to zdarzenia z dokładnie jedną szóstką na pierwszym lub drugim miejscu. Mamy zatem
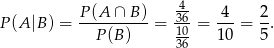
Odpowiedź: 
