Zadanie nr 6603271
Oblicz prawdopodobieństwo warunkowe, że w czterokrotnym rzucie symetryczną sześcienną kostką do gry otrzymamy co najmniej dwie „dwójki”, pod warunkiem że otrzymamy co najmniej jedną „piątkę”.
Rozwiązanie
Za zdarzenia elementarne przyjmijmy uporządkowane czwórki wylosowanych oczek. Mamy więc
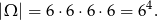
Niech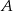 
oznacza zdarzenie polegające na otrzymaniu co najmniej dwóch dwójek, a 
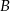zdarzenie polegające na otrzymaniu co najmniej jednej piątki. Musimy obliczyć
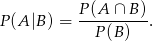
Prawdopodobieństwo zdarzenia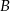 
łatwo obliczyć jeżeli przejdziemy do zdarzenia przeciwnego 
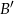. Zdarzenia sprzyjające 
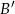, to takie, w których na żadnej z kostek nie ma piątki. Jest więc 
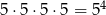takich zdarzeń i
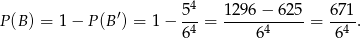
Zdarzenia sprzyjające zdarzeniu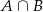 
(czyli otrzymaniu co najmniej dwóch dwójek i co najmniej jednej piątki) możemy podzielić na trzy typy:
– wylosowaliśmy 3 dwójki i 1 piątkę – są cztery takie zdarzenia (piątkę możemy otrzymać na jednej z czterech kostek);
– wylosowaliśmy 2 dwójki i 2 piątki – jest
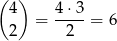
takich zdarzeń (wybieramy miejsca dla dwójek, a na pozostałych umieszczamy piątki);
– wylosowaliśmy 2 dwójki, 1 piątkę i jedną liczbę różną od 2 i 5 – takich zdarzeń jest
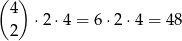
(wybieramy dwa miejsca dla dwójek, miejsce dla piątki i jedną z czterech pozostałych liczb, którą umieszczamy na pozostałej kostce).
Mamy więc
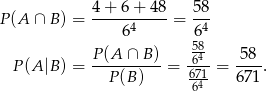
Odpowiedź: 
