Zadanie nr 7426904
Rzucamy dwa razy kostką do gry. Jeśli suma oczek wyrzuconych na obu kostkach jest liczbą podzielną przez 3, losujemy jedną liczbę ze zbioru 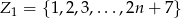 , w przeciwnym przypadku losujemy jedną liczbę ze zbioru
, w przeciwnym przypadku losujemy jedną liczbę ze zbioru 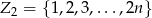 . Oblicz prawdopodobieństwo wylosowania liczby parzystej.
. Oblicz prawdopodobieństwo wylosowania liczby parzystej.
Rozwiązanie
Ustalmy, że zdarzeniem elementarnym przy dwukrotnym rzucie kostką jest uporządkowana para otrzymanych wyników. Zatem
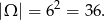
Jeżeli oznaczymy zdarzenia
A – suma oczek wyrzuconych na obu kostkach jest liczbą podzielną przez 3
B=A’ – suma oczek wyrzuconych na obu kostkach nie jest liczbą podzielną przez 3,
to zdarzenia sprzyjające do 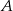 to
to
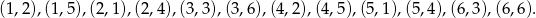
Zatem
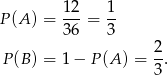
Niech 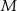 oznacza zdarzenie polegające na wylosowaniu liczby parzystej (w wyniku całego opisanego doświadczenia, czyli najpierw rzucamy kostkami, potem losujemy liczby). Prawdopodobieństwo wylosowania liczby parzystej ze zbioru
oznacza zdarzenie polegające na wylosowaniu liczby parzystej (w wyniku całego opisanego doświadczenia, czyli najpierw rzucamy kostkami, potem losujemy liczby). Prawdopodobieństwo wylosowania liczby parzystej ze zbioru 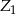 wynosi
wynosi
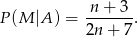
W zbiorze 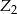 jest tyle samo liczb parzystych co nieparzystych, zatem
jest tyle samo liczb parzystych co nieparzystych, zatem
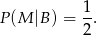
Korzystamy teraz ze wzoru na prawdopodobieństwo całkowite.
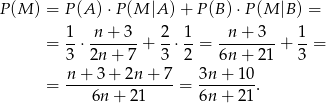
Odpowiedź: