/Szkoła średnia/Prawdopodobieństwo/Warunkowe i całkowite/Kostki

Zadanie nr 8616202

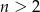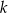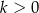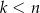W pudełku znajduje się n > 2 sześciennych kostek do gry, przy czym k spośród tych kostek (k > 0 i k < n ) ma na dwóch ściankach jedno oczko, a na pozostałych czterech ściankach sześć oczek. Wybieramy losowo jedną z tych kostek i wykonujemy nią cztery kolejne rzuty. Oblicz jakie jest prawdopodobieństwo, że wybrana kostka miała jedno oczko na dwóch ściankach, jeżeli wiadomo, że w każdym z czterech wykonanych rzutów otrzymano ściankę z sześcioma oczkami.

Wersja PDF

Rozwiązanie

Prawdopodobieństwo wyrzucenia czterech kolejnych szóstek przy rzucie zwykłą kostką jest równe

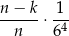
n-−-k-⋅ 1-- n 64

(zwykłą kostkę możemy wybrać z prawdopodobieństwem 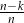n−k -n-- , a potem jest tylko jedno zdarzenie sprzyjające) Analogicznie, prawdopodobieństwo otrzymania czterech kolejnych szóstek przy rzucie zmodyfikowaną kostką jest równe

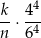
k 44 --⋅ -4- n 6

(zmodyfikowaną kostkę możemy wybrać na 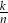k n sposobów, a potem prawdopodobieństwo otrzymania czterech szóstek jest równe 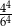4 464 – przy każdym rzucie wybieramy jedną z 4 ścianek z sześcioma oczkami).

Wśród wszystkich możliwych zdarzeń, w których wypadły cztery szóstki zdarzenia odpowiadające zmodyfikowanej kostce stanowią więc

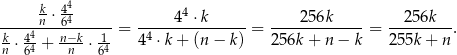
k 44 4 -----n-⋅64------= -----4-⋅k------= ----256k-----= --256k---. k ⋅ 44+ n−k-⋅ 1 44 ⋅k + (n − k) 256k + n − k 255k + n n 64 n 64

Jeżeli chcemy zapisać powyższy rachunek przy pomocy prawdopodobieństwa warunkowego, to oznaczmy przez 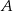A zdarzenie polegające na wybraniu zmodyfikowanej kostki, a przez 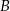B zdarzenie polegające na wyrzuceniu 4 kolejnych szóstek. Przy tych oznaczeniach interesujące nas prawdopodobieństwo to prawdopodobieństwo warunkowe

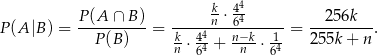
k ⋅ 44 P(A |B) = P(A-∩--B)-= -----n--64------= --256k---. P(B ) k ⋅ 444 + n−k-⋅-14 255k + n n 6 n 6

 
Odpowiedź: --256k- 255k+n

Wersja PDF