Zadanie nr 9105618
Rzucamy sześcienną kostką do gry tak długo, aż otrzymamy co najmniej dwie nieparzyste liczby oczek, albo 10 parzystych liczb oczek. Oblicz prawdopodobieństwo, że w przeprowadzonym doświadczeniu otrzymaliśmy liczbę oczek równą 5, przy założeniu, że otrzymaliśmy tylko jedną nieparzystą liczbę oczek.
Rozwiązanie
Sposób I
Skoro wiemy, że wyrzuciliśmy tylko jedną nieparzystą liczbę oczek, to z podanego opisu wynika, że musieliśmy rzucać kostką 11 razy i wszystkie pozostałe rzuty dały parzyste liczby oczek. Jest więc
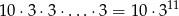
zdarzeń elementarnych (najpierw wybieramy w którym rzucie ma być liczba nieparzysta (nie może być w ostatnim) i w każdym rzucie mamy do wyboru jedną z trzech liczb – w jednym musi to być liczba nieparzysta, a w pozostałych parzyste).
Zdarzeń sprzyjających jest
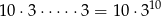
(wybieramy, w którym rzucie ma być liczba 5, a w którym z pozostałych otrzymujemy liczbę parzystą),
Prawdopodobieństwo jest więc równe
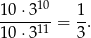
Sposób II
Wiemy, że została wylosowana dokładnie jedna liczba nieparzysta i musi to być jedna z liczb: 1, 3 lub 5. Ponieważ żadna z tych liczb nie jest w żaden sposób wyróżniona, jest dokładnie tyle samo zdarzeń, w których wylosowana jest każda z tych liczb. Prawdopodobieństwo jest więc równe 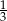 .
.
Sposób III
Tym skorzystamy ze wzoru na prawdopodobieństwo warunkowe – niech 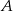 oznacza zdarzenie polegające na wyrzuceniu piątki, a
oznacza zdarzenie polegające na wyrzuceniu piątki, a 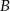 zdarzenie polegające na wyrzuceniu dokładnie jednej liczby nieparzystej.
zdarzenie polegające na wyrzuceniu dokładnie jednej liczby nieparzystej.
Ponieważ będziemy liczyć iloraz prawdopodobieństw (ze wzoru na prawdopodobieństwo warunkowe), nie jest nam potrzebna znajomość liczby zdarzeń elementarnych – powiedzmy, że jest ich  .
.
Zdarzeń sprzyjających zdarzeniu 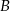 jest
jest
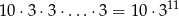
(najpierw wybieramy, w którym rzucie ma być liczba nieparzysta (nie może być w ostatnim ) i w każdym rzucie mamy do wyboru jedną z trzech liczb – w jednym musi to być liczba nieparzysta, a w pozostałych parzyste).
Zdarzeń sprzyjających zdarzeniu 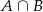 jest
jest
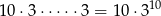
(wybieramy, w którym rzucie ma być liczba 5, a w każdym z pozostałych rzutów umieszczamy liczbę parzystą).
Interesujące nas prawdopodobieństwo jest więc równe
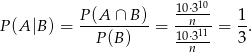
Odpowiedź: