Zadanie nr 2225077
Ze zbioru liczb 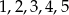 losujemy kolejno trzy razy po jednej liczbie bez zwracania tworząc liczbę trzycyfrową. Oblicz prawdopodobieństwo zdarzenia
losujemy kolejno trzy razy po jednej liczbie bez zwracania tworząc liczbę trzycyfrową. Oblicz prawdopodobieństwo zdarzenia 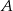 – otrzymana liczba jest mniejsza od 432.
– otrzymana liczba jest mniejsza od 432.
Rozwiązanie
Przyjmijmy, że zdarzenia elementarne to trójki wylosowanych cyfr, czyli
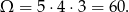
Jeżeli wylosowana liczba ma być mniejsza od 432, to mamy trzy możliwości.
Jeżeli pierwsza cyfra jest mniejsza od 4, to pozostałe dwie cyfry mogą być dowolne. Jest
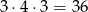
takich liczb (pierwszą cyfrę wybieramy na 3 sposoby, drugą na 4, trzecią na 3).
Jeżeli pierwsza cyfra jest równa 4 i druga jest równa 1 lub 2, to trzecia cyfra jest dowolna, więc jest
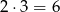
takich liczb.
Jeżeli pierwsza cyfra jest równa 4, a druga jest równa 3, to trzecia musi być równa 1. Jest więc jedna taka liczba.
W sumie są więc
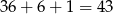
liczby spełniające warunki zadania i prawdopodobieństwo jest równe
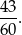
Odpowiedź: