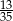/Szkoła średnia/Prawdopodobieństwo/Z definicji/Zbiory liczb/Własności cyfr

Zadanie nr 2759096

Dodaj do ulubionych
Dodaj do rozwiązanych

Ze zbioru 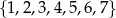{1,2,3,4,5,6,7 } losujemy kolejno, bez zwracania trzy cyfry i tworzymy liczbę trzycyfrową: pierwsza wylosowana cyfra jest cyfrą setek, druga – cyfrą dziesiątek, a trzecia – cyfrą jedności. Oblicz prawdopodobieństwo zdarzenia, że otrzymana liczba ma następującą własność: różnica między największą i najmniejszą cyfrą tej liczby jest nie większa niż 3.

Rozwiązanie

Jeżeli za zdarzenia elementarne przyjmiemy trójki wylosowanych liczb to

|Ω | = 7⋅6 ⋅5.

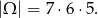
Zastanówmy się ile jest zdarzeń sprzyjających. Ponieważ losujemy trzy różne cyfry i każda permutacja wyniku daje prawidłową liczbę, wystarczy policzyć ile jest ’dobrych’ wyborów trójek 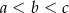a < b < c , na koniec otrzymaną liczbę pomnożymy przez liczbę wszystkich możliwych permutacji, czyli przez 3! = 6 .

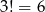Liczby 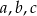a,b,c są różne, więc różnica między największą i najmniejszą jest równa co najmniej 2. Z drugiej strony ma być ona nie większa niż 3. Łatwo wypisać wszystkie możliwe wybory z c − a = 2 :

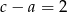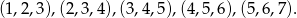
(1,2,3),(2,3,4),(3,4,5),(4,5,6 ),(5,6,7).

Wyborów z 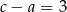c− a = 3 jest trochę więcej

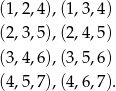
(1,2,4),(1,3,4) (2,3,5),(2,4,5) (3,4,6),(3,5,6) (4,5,7),(4,6,7).

W sumie jest więc 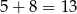5+ 8 = 13 trójek spełniających warunek 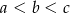a < b < c . Wszystkich zdarzeń sprzyjających jest zatem

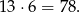
1 3⋅6 = 78.

Prawdopodobieństwo jest równe

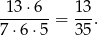
13 ⋅6 13 ------- = --. 7 ⋅6 ⋅5 35

 
Odpowiedź: 13 35

Wersja PDF