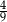/Szkoła średnia/Prawdopodobieństwo/Z definicji/Zbiory liczb/Własności cyfr

Zadanie nr 5400971

Spośród cyfr 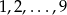1,2,...,9 losujemy bez zwracania dwie i tworzymy z nich liczbę dwucyfrową, której cyfrą dziesiątek jest pierwsza z wylosowanych cyfr. Oblicz prawdopodobieństwo że otrzymana liczba jest parzysta.

Wersja PDF

Rozwiązanie

Skoro losujemy bez zwracania, to możemy dwie tę liczbę wylosować na

|Ω | = 9 ⋅8

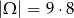
sposobów.

Sposób I

Liczba będzie parzysta jeżeli druga cyfra jest parzysta. Możemy ją wybrać na 4 sposoby (2,4,6 lub 8). Do tego pierwszą cyfrę mnożemy wybrać na 8 sposobów (ma być różna od drugiej). Prawdopodobieństwo wynosi więc

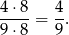
4-⋅8 4- 9 ⋅8 = 9.

Sposób II

Tym razem najpierw popatrzmy jaka jest pierwsza wylosowana cyfra, a potem jaka jest druga.

Jeżeli pierwsza wylosowana cyfra jest nieparzysta (co może się zdarzyć na 5 sposobów), to drugą cyfrę parzystą możemy wylosować na 4 sposoby. Mamy więc w tym przypadku 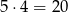5 ⋅4 = 2 0 zdarzeń sprzyjających.

Jeżeli pierwsza wylosowana cyfra jest parzysta (co może się zdarzyć na 4 sposoby), to drugą cyfrę parzystą możemy wylosować już tylko na 3 sposoby. Mamy więc w tym przypadku 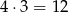4⋅3 = 12 zdarzeń sprzyjających.

Prawdopodobieństwo wynosi więc

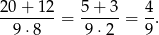
20-+-12-= 5-+-3-= 4. 9 ⋅8 9⋅ 2 9

 
Odpowiedź: 4 9

Wersja PDF