Zadanie nr 5766657
Z cyfr 0, 1, 2, 3, 4 układamy wszystkie możliwe liczby trzycyfrowe o różnych cyfrach. Ze zbioru takich liczb losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia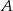 
– wybrana liczba trzycyfrowa ma tę własność, że cyfry: setek, dziesiątek oraz jedności (w podanej kolejności) tworzą ciąg arytmetyczny.
Rozwiązanie
W podanym zbiorze jest
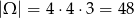
liczb (pierwszą możemy wybrać na 4 sposoby, drugą też na 4, a trzecią na 3).
Policzmy zdarzenia sprzyjające. Cyfr nie jest zbyt dużo, więc możemy wypisać wszystkie możliwości
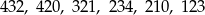
Prawdopodobieństwo wynosi więc
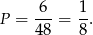
Odpowiedź: 
