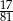Zadanie nr 6241925
Z cyfr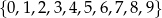 
losujemy 3 cyfry i zapisujemy z ich pomocą liczbę 3-cyfrową o niepowtarzających się cyfrach, przy czym zakładamy, że pierwsza cyfra jest niezerowa. Oblicz prawdopodobieństwo otrzymania liczby podzielnej przez 5.
Rozwiązanie
Wszystkich liczb, które można utworzyć z podanych cyfr jest
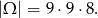
(pierwszą cyfrę musi być różna od 0, druga musi być różna od pierwszej, a trzecia od dwóch pierwszych).
Aby liczba była podzielna przez 5, jej ostatnia cyfra musi być równa 0 lub 5. Jeżeli ostatnia cyfra jest równa 0, to pierwsze dwie można wybrać na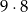 
sposobów (bo nie ma problemu z zerem na początku). Jeżeli natomiast ostatnia cyfra jest równa 5, to mamy 
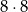sposobów. Prawdopodobieństwo wynosi więc
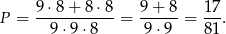
Odpowiedź: 
