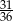Zadanie nr 6275345
Ze zbioru liczb trzycyfrowych losujemy jedną liczbę. Jakie jest prawdopodobieństwo, że iloczyn cyfr wylosowanej liczby jest liczbą parzystą?
Rozwiązanie
Wszystkich liczb trzycyfrowych jest
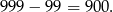
Zamiast liczyć, ile jest liczb spełniających warunki zadania obliczmy, ile jest liczb, które tych warunków nie spełniają. W takich liczbach wszystkie cyfry muszą być nieparzyste, więc jest
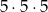
takich liczb (każda cyfra jest jedną z 5 cyfr nieparzystych). Interesujące nas prawdopodobieństwo jest więc równe
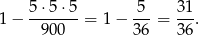
Odpowiedź: