Zadanie nr 6507228
Ze zbioru liczb trzycyfrowych, które nie mają dwóch takich samych cyfr losujemy jedną liczbę. Jakie jest prawdopodobieństwo otrzymania liczby, której iloczyn cyfr jest liczbą niezerową podzielną przez 7?
Rozwiązanie
Jeżeli liczba trzycyfrowa ma mieć wszystkie cyfry różne, to pierwszą cyfrę możemy wybrać na 9 sposobów (nie może być 0), drugą też na 9 sposobów (nie może być taka jak pierwsza), a trzecią na 8 sposobów (musi być różna od dwóch pierwszych). Zatem
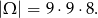
Jeżeli iloczyn cyfr ma dzielić się przez 7, to jedna z cyfr musi być równa 7. Ponadto wśród cyfr nie może być zera.
Cyfra 7 może być na jednej z trzech pozycji, a gdy już ustalimy tę pozycję, to pozostałe dwie cyfry możemy wybrać na
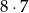
sposobów (druga cyfra musi być różna od 0 i 7, a trzecia dodatkowo musi być różna od drugiej). Łącznie jest więc
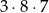
takich liczb i prawdopodobieństwo wynosi
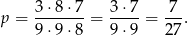
Odpowiedź: