Zadanie nr 6822352
Ze zbioru wszystkich liczb naturalnych trzycyfrowych losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia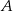 
polegającego na tym, że wylosowana liczba jest podzielna przez 4 oraz ma dwie cyfry nieparzyste.
Rozwiązanie
Wszystkich liczb trzycyfrowych jest
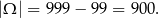
Liczba jest podzielna przez 4, jeżeli liczba dwucyfrowa utworzona z jej dwóch ostatnich cyfr jest podzielna przez 4. Wiemy ponadto, że w interesujących nas liczbach może być tylko jedna cyfra parzysta, więc każda taka liczba musi się kończyć jedną z 10 końcówek:
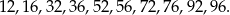
Do tego pierwszą cyfrę możemy wybrać na 5 sposobów (musi być nieparzysta). Jest więc
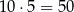
liczb trzycyfrowych spełniających warunki zadania i interesujące nas prawdopodobieństwo jest równe
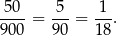
Odpowiedź: 
