Zadanie nr 7167434
Spośród liczb naturalnych sześciocyfrowych wybieramy jedną liczbę. Jakie jest prawdopodobieństwo wybrania liczby, której iloczyn cyfr jest podzielny przez 9, jeżeli wiadomo, że każda cyfra wylosowanej liczby jest większa od 1?
Rozwiązanie
Tak naprawdę mamy do czynienia z prawdopodobieństwem warunkowym, ale najprościej będzie od razu zajmować się tylko takimi zdarzeniami, w których każda cyfra jest większa od 1. Jest
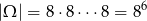
liczb sześciocyfrowych spełniających ten warunek.
Jeżeli się chwilę zastanowimy, to powinno stać się jasne, że jest dość dużo możliwości otrzymania liczby z iloczynem cyfr podzielnym przez 9, więc zamiast zajmować się zdarzeniem opisanym w treści zadania, zajmijmy się zdarzeniem przeciwnym, gdy iloczyn cyfr nie dzieli się przez 9.
Są dwa rodzaje takich zdarzeń: albo żadna z cyfr nie dzieli się przez 3, albo dokładnie jedna z cyfr jest trójką lub szóstką. Zdarzeń pierwszego rodzaju jest
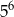
(każdą cyfrę wybieramy spośród: 2, 4, 5, 7, 8), a zdarzeń drugiego rodzaju jest
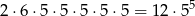
(na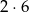 
sposobów wybieramy trójkę lub szóstkę oraz miejsce tej cyfry, a potem na 
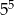sposobów umieszczamy na pozostałych miejscach cyfry niepodzielne przez 3).
Interesujące nas prawdopodobieństwo jest więc równe
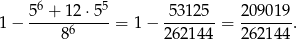
Odpowiedź: 
