/Szkoła średnia/Prawdopodobieństwo/Z definicji/Zbiory liczb/Własności cyfr

Zadanie nr 8682690

Ze zbioru wszystkich liczb naturalnych ośmiocyfrowych, w których zapisie dziesiętnym występują tylko cyfry ze zbioru 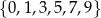{0,1,3,5,7,9 } , losujemy jedną. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że suma cyfr wylosowanej liczby jest równa 3.

Wersja PDF

Rozwiązanie

Wszystkich liczb ośmiocyfrowych o cyfrach ze zbioru 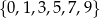{ 0,1,3,5,7,9} jest

5⋅67

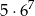
(pierwszą cyfrę wybieramy na 5 sposobów – nie może być zerem, a każdą z pozostałych cyfr wybieramy na 6 sposobów).

Wśród tych liczb są dwa rodzaje liczb o sumie cyfr równej 3: liczba

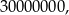
300 00000,

oraz liczby, w których jedyne niezerowe cyfry to trzy jedynki. Liczb z trzema jedynkami jest

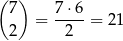
( ) 7 7 ⋅6 = ---- = 2 1 2 2

(jedna jedynka musi być na początku, a pozostałe dwie umieszczamy na dwóch spośród 7 pozostałych cyfr). Interesujące nas prawdopodobieństwo jest więc równe

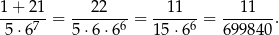
1+--21-= --2-2---= --11-- = --11---. 5⋅67 5⋅ 6⋅66 15 ⋅66 699840

 
Odpowiedź: 69191840

Wersja PDF