Ile jest wszystkich liczb trzycyfrowych? Można to obliczyć na różne sposoby, np. wypisując te liczby

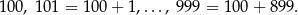
Liczb trzycyfrowych jest zatem tyle, ile jest liczb od 0 do 899, czyli 900.

Inny sposób jest następujący: pierwszą cyfrę możemy wybrać na 9 sposobów (bo nie może być 0), a drugą i trzecią na 10 sposobów. Jest więc

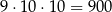
takich liczb.

Ile jest liczb z różnymi cyframi? - pierwszą cyfrę takiej liczby możemy wybrać na 9 sposobów (nie może być 0). Drugą też na 9 sposobów (bo nie może być cyfra, którą napisaliśmy na pierwszym miejscu), a trzecią na 8 sposobów (bo mamy już dwie cyfry zajęte). Zatem prawdopodobieństwo wynosi

 
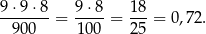
Odpowiedź: 0,72