Zadanie nr 1425042
Spośród liczb naturalnych trzycyfrowych wybieramy jedną liczbę. Jakie jest prawdopodobieństwo wybrania liczby, która przy dzieleniu przez 11 daje resztę 3.
Rozwiązanie
Ponieważ
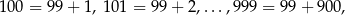
to wszystkich liczb trzycyfrowych jest 900. Zatem
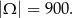
Podobnie obliczamy liczbę wszystkich liczb trzycyfrowych, które przy dzieleniu przez 11 dają resztę 3.
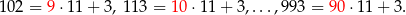
Jest ich więc 90-8=82 (liczba liczb pomiędzy 9 a 90). Zatem szukane prawdopodobieństwo wynosi
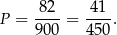
Odpowiedź: