Zadanie nr 3648784
Ze zbioru liczb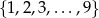 
losujemy kolejno dwa razy po jednej liczbie (liczby mogą się powtarzać). Oblicz prawdopodobieństwo wylosowania liczb, których suma jest podzielna przez 5.
Rozwiązanie
Jeżeli za zdarzenia elementarne przyjmiemy pary wylosowanych liczb, to
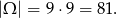
Wypiszmy zdarzenia sprzyjające (suma wylosowanych liczb musi być równa 5 ,10 lub 15):
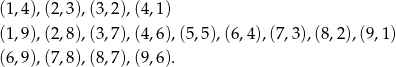
Prawdopodobieństwo jest więc równe
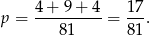
Odpowiedź: 
