/Szkoła średnia/Prawdopodobieństwo/Z definicji/Zbiory liczb/Podzielność

Zadanie nr 4226681

Z cyfr 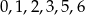0,1,2,3,5,6 tworzymy liczbę czterocyfrową, przy czym cyfry nie mogą się powtarzać. Jakie jest prawdopodobieństwo otrzymania liczby podzielnej przez 25?

Wersja PDF

Rozwiązanie

Ile różnych liczb czterocyfrowych możemy utworzyć? – na pierwszym miejscu musi być cyfra niezerowa więc możemy ją wybrać na 5 sposobów, drugą cyfrę możemy wybrać też na 5 sposobów (musi być różna od pierwszej cyfry), trzecią na 4 sposoby i ostatnią na 3. Razem mamy

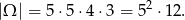
|Ω | = 5⋅5 ⋅4 ⋅3 = 52 ⋅12.

Teraz musimy obliczyć zdarzenia sprzyjające. Liczba jest podzielna przez 25 jeżeli jej ostatnie dwie cyfry to 00,25,50 lub 75. W naszej sytuacji możliwe są tylko końcówki 25 i 50.

Jeżeli na końcu mamy 25, to pierwszą cyfrę możemy wybrać na 3 sposoby (nie może być 0,2,5) i drugą też na 3 sposoby.

Jeżeli na końcu jest 50, to pierwszą cyfrę możemy wybrać na 4 sposoby, a drugą na 3. W sumie daje to nam

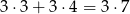
3 ⋅3+ 3⋅ 4 = 3⋅ 7

sposobów. Zatem prawdopodobieństwo wynosi

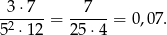
3⋅7 7 -2----= ------= 0,07. 5 ⋅12 25 ⋅4

 
Odpowiedź: 0,07

Wersja PDF