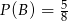/Szkoła średnia/Prawdopodobieństwo/Z definicji/Zbiory liczb/Podzielność

Zadanie nr 5516090

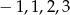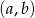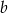W pudełku są cztery kartki, na których wypisano liczby − 1,1,2,3 (na każdej kartce jedną liczbę). Losujemy jedną kartkę, zapisujemy liczbę i zwracamy kartkę do pudełka. Następnie losujemy drugą kartkę i zapisujemy liczbę. Wylosowane liczby tworzą parę (a,b) , gdzie a jest liczbą wylosowaną za pierwszym razem, zaś b liczbą wylosowaną za drugim razem. Oblicz prawdopodobieństwo zdarzenia

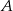  • A – iloczyn wylosowanych liczb jest liczbą pierwszą;
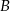  • B – różnica wylosowanych liczb jest liczbą parzystą.
Wersja PDF

Rozwiązanie

Losujemy dwa razy ze zwracaniem ze zbioru, który ma cztery elementy, więc

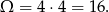
Ω = 4⋅4 = 16.
  • Liczba pierwsza jest to taka liczba naturalna większa od 1 która nie ma żadnych dzielników poza 1 i samą sobą. Wypisujemy zdarzenia sprzyjające
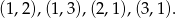
    (1 ,2),(1,3),(2,1),(3,1).

    Stąd prawdopodobieństwo wynosi

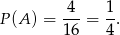
    4 1 P (A ) = ---= -. 16 4

     
    Odpowiedź: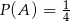 P(A ) = 14

  • Wypiszmy zdarzenia sprzyjające
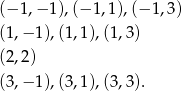
    (− 1,− 1),(− 1,1),(− 1,3) (1,− 1),(1,1),(1,3) (2,2) (3,− 1),(3,1),(3,3).

    Zatem prawdopodobieństwo wynosi

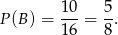
    10 5 P (B) = ---= -. 16 8

     
    Odpowiedź: P(B ) = 5 8

Wersja PDF