Zadanie nr 5615556
Ze zbioru liczb 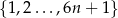 ,
, 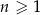 losujemy kolejno trzy razy po jednej liczbie bez zwracania. Niech
losujemy kolejno trzy razy po jednej liczbie bez zwracania. Niech 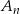 oznacza zdarzenie polegające na tym, że iloczyn wylosowanych liczb jest podzielny przez 6. Oblicz granicę
oznacza zdarzenie polegające na tym, że iloczyn wylosowanych liczb jest podzielny przez 6. Oblicz granicę 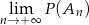 .
.
Rozwiązanie
Jest
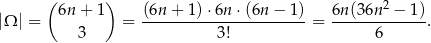
zdarzeń elementarnych.
Zauważmy jeszcze, że wśród podanych liczb jest  liczb podzielnych przez 6:
liczb podzielnych przez 6:
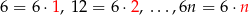
Jest 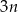 liczb parzystych
liczb parzystych
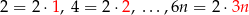
oraz 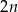 liczb podzielnych przez 3:
liczb podzielnych przez 3:
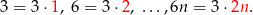
Łatwo też na podstawie powyższej obserwacji ustalić, że w danym zbiorze jest
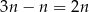
liczb parzystych, które nie dzielą się przez 3 (bo jak dzielą się przez 2 i 3, to dzielą się przez 6). Analogicznie, jest
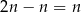
liczb podzielnych przez 3, które nie dzielą się przez 2. Pozostałe
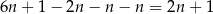
liczby nie dzielą się ani przez 2, ani przez 3 (ze zbioru wszystkich liczb wyrzucamy te, które dzielą się przez 6, te które dzielą się przez 2, ale nie przez 3, i w końcu te które dzielą się przez 3, ale nie dzielą się przez 2).
Sposób I
Jeżeli chwilę zastanowimy się nad treścią zadania, to powinno być jasne, że jest bardzo dużo zdarzeń sprzyjających, więc spróbujmy zastanowić się nad zdarzeniem przeciwnym do 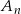 , czyli takim, w którym iloczyn otrzymanych liczb nie dzieli się przez 6.
, czyli takim, w którym iloczyn otrzymanych liczb nie dzieli się przez 6.
Układów, w których nie ma liczby podzielnej przez 3 jest
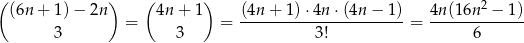
Układów, w których nie ma liczby parzystej jest
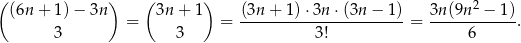
W tym miejscu łatwo popełnić błąd – zauważmy, że w powyższym rachunku układy, w których nie ma ani liczby podzielnej przez 3, ani przez 2 policzyliśmy podwójnie. Takich układów jest
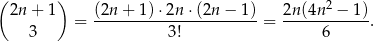
Interesujące nas prawdopodobieństwo jest więc równe
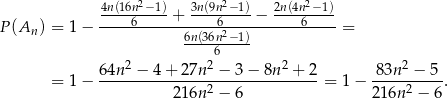
Liczymy granicę z tego wyrażenia
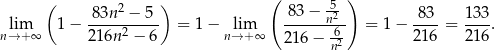
Sposób II
Tym razem spróbujmy obliczyć liczbę zdarzeń sprzyjających wprost – bez patrzenia na zdarzenie przeciwne.
Zdarzeń, w których jest przynajmniej jedna liczba podzielna przez 6 jest
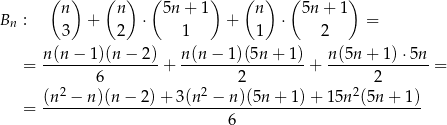
(mogą być trzy, dwie albo jedna liczba podzielna przez 6).
Jeżeli nie ma liczby podzielnej przez 6, to musi być przynajmniej jedna parzysta i jedna podzielna przez 3. Znowu jest kilka możliwości – żeby się nie pogubić najlepiej myśleć o trzeciej liczbie – może być parzysta, może być podzielna przez 3, albo może być względnie pierwsza z 6. Jest więc
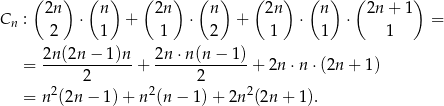
Pozostało obliczyć interesującą nas granicę.
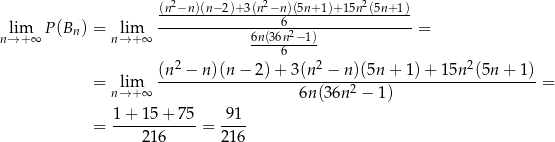
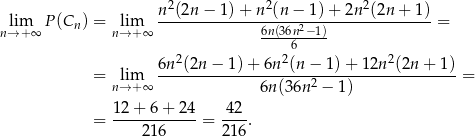
Stąd
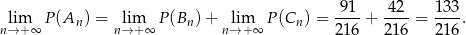
Odpowiedź: