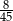Zadanie nr 6156025
Ze zbioru liczb naturalnych dwucyfrowych losowo wybieramy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia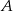 
polegającego na tym, że otrzymamy liczbę podzielną przez 9 lub liczbę podzielną przez 12.
Rozwiązanie
Liczb dwucyfrowych jest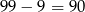 
, więc
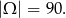
Sposób I
Liczby dwucyfrowe podzielne przez 9 to:
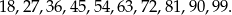
Jak widać jest ich 10.
Liczby dwucyfrowe podzielne przez 12 to:
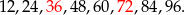
Jest ich 8, ale 2 z nich występują na poprzedniej licie. Prawdopodobieństwo jest więc równe
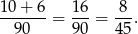
Sposób II
Liczby podzielne przez 9 to liczby
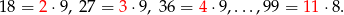
Jest ich zatem 10. Podobnie liczymy liczbę liczb podzielnych przez 12
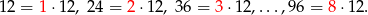
Jest ich 8.
Doszliśmy teraz do delikatnego momentu, jeżeli dodamy do siebie wyliczone liczby, to nie będzie to liczba liczb podzielnych przez 9 lub 12. Powód jest prosty: liczby które są podzielne jednocześnie przez 9 i 12 (czyli przez 36) policzyliśmy podwójnie. Musimy zatem od tej sumy odjąć liczbę liczb podzielnych przez 36. Są 2 takie liczby:
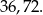
Możemy już obliczyć szukane prawdopodobieństwo
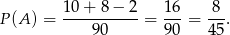
Odpowiedź: 
