Spośród liczb: 0, 1, 2, 3, 4, 5,…, 1000 wybieramy losowo jedną liczbę. Oblicz prawdopodobieństwo zdarzenia, że liczba ta jest podzielna przez 4 lub 5.
Wszystkich zdarzeń elementarnych jest oczywiście 1001, zatem
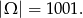
Liczby podzielne przez 4 to liczby
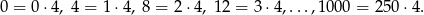
Jest ich zatem 251. Podobnie liczymy ilość liczb podzielnych przez 5
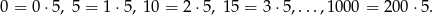
Jest ich 201.
Doszliśmy teraz do delikatnego momentu, jeżeli dodamy do siebie wyliczone ilości, to nie będzie to ilość liczb podzielnych przez 4 lub 5. Powód jest prosty, liczby które są podzielne jednocześnie przez 4 i 5 (czyli przez 20) policzyliśmy podwójnie. Musimy zatem od tej sumy odjąć ilość liczb podzielnych przez 20. Policzmy je.
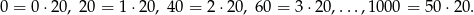
Jest ich zatem 51.
Możemy już policzyć szukane prawdopodobieństwo
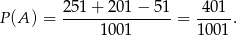
Odpowiedź: 
Informacje
Zadania
Losowe zadanie
