/Szkoła średnia/Prawdopodobieństwo/Z definicji/Zbiory liczb/Podzielność

Zadanie nr 6799759

Dodaj do ulubionych
Dodaj do rozwiązanych

Na sześciu jednakowych kartkach napisano liczby: 1, 10, 100, 1000, 10000, 100000. Z tych kartek losujemy kolejno bez zwracania trzy. Oblicz prawdopodobieństwo, że suma wylosowanych liczb tworzy liczbę podzielną przez cztery.

Rozwiązanie

Sposób I

Trzy liczby z 6 możemy wylosować na

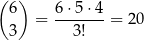
( ) 6 = 6⋅-5⋅4-= 20 3 3!

sposobów. Jeżeli liczba utworzona z wylosowanych liczb ma być podzielna przez 4, to wśród tych liczb nie może być 1 i nie może być 10. Są więc

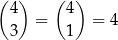
(4) ( 4) = = 4 3 1

sposoby utworzenia takiej liczby. Interesujące nas prawdopodobieństwo jest więc równe

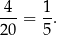
-4-= 1. 20 5

Sposób II

Wypiszmy wszystkie liczby jakie możemy otrzymać w wyniku opisanego losowania

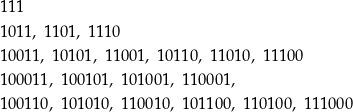
111 1011, 1101, 1110 10011, 10101 , 1100 1, 10 110, 11010, 11100 100011, 1001 01, 10 1001, 110001 , 100110, 1010 10, 11 0010, 101100 , 110 100, 1 11000

Jest więc 20 takich liczb. Liczby podzielne prze 4 na tej liście to liczby kończące się dwoma zerami – są 4 takie liczby. Interesujące nas prawdopodobieństwo jest więc równe

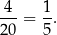
-4-= 1. 20 5

 
Odpowiedź: 15

Wersja PDF