/Szkoła średnia/Prawdopodobieństwo/Z definicji/Zbiory liczb/Podzielność

Zadanie nr 7038034

Dodaj do ulubionych
Dodaj do rozwiązanych

Ze zbioru sześciu liczb 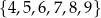{4,5,6 ,7,8,9} losujemy ze zwracaniem kolejno dwa razy po jednej liczbie. Oblicz prawdopodobieństwo zdarzenia 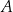A polegającego na tym, że iloczyn wylosowanych liczb jest podzielny przez 9.

Rozwiązanie

Rozwiązanie tego zadania jest dostępne tylko dla użytkowników z wykupionym abonamentem.
Zaloguj się Informacje o abonamencie
Nie chcesz się rejestrować ani opłacać abonamentu? Zapłać przelewem 7,90 zł lub telefonicznie 9,90 zł, a otrzymasz dwudziestominutowy dostęp do wszystkich materiałów dostępnych w portalu.