Zadanie nr 8177613
Ze zbioru liczb 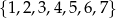 losujemy trzy razy po jednej liczbie bez zwracania. Oblicz prawdopodobieństwo zdarzenia
losujemy trzy razy po jednej liczbie bez zwracania. Oblicz prawdopodobieństwo zdarzenia 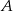 , polegającego na wylosowaniu liczb, których iloczyn jest podzielny przez 4.
, polegającego na wylosowaniu liczb, których iloczyn jest podzielny przez 4.
Rozwiązanie
Za zdarzenia elementarne przyjmijmy trójki wylosowanych liczb. Mamy zatem
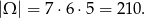
Jeżeli jedną z wylosowanych liczb jest 4, to pozostałe dwie liczby mogą być dowolne (ale różne od siebie i od 4). Obliczmy ile jest ciągów tej postaci: czwórka może stać na jednym z trzech miejsc, a pozostałe dwie liczby możemy wybrać na 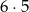 sposobów. W sumie jest więc
sposobów. W sumie jest więc
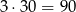
zdarzeń tego typu.
Jeżeli wśród wylosowanych liczb nie ma 4-tki, to jedną z nich musi być 2 i jedną z pozostałych musi być 6. Dwójkę możemy umieścić na 3 sposoby, szóstkę na 2, a ostatnią liczbę możemy wybrać na 4 sposoby. Są więc
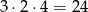
takie trójki.
W sumie jest więc
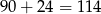
zdarzeń sprzyjających i prawdopodobieństwo wynosi
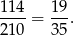
Odpowiedź: