/Szkoła średnia/Prawdopodobieństwo/Z definicji/Zbiory liczb/Podzielność

Zadanie nr 8255435

Ze zbioru liczb całkowitych spełniających nierówność 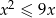2 x ≤ 9x losujemy dwie różne liczby. Wylosowanie każdej liczby z tego zbioru jest jednakowo prawdopodobne. Oblicz prawdopodobieństwo wylosowania dwóch liczb pierwszych.

Wersja PDF

Rozwiązanie

Rozwiążmy najpierw podaną nierówność

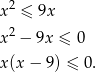
2 x ≤ 9x x 2 − 9x ≤ 0 x (x− 9) ≤ 0.

Losujemy zatem wśród liczb całkowitych z przedziału 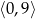⟨0,9⟩ , czyli ze zbioru

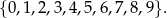
{ 0,1,2,3,4,5,6,7,8 ,9}.

Liczy pierwsze w tym przedziale to 2,3,5 i 7. Szukane prawdopodobieństwo wynosi więc

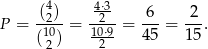
(4) 4⋅3- 6 2 P = -210--= 120⋅9-= ---= ---. (2) -2-- 45 15

 
Odpowiedź: -2 15

Wersja PDF